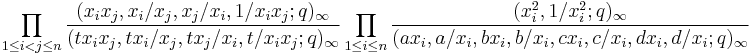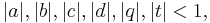Koornwinder polynomials

In mathematics, Koornwinder polynomials (also called Macdonald-Koornwinder polynomials) are a family of orthogonal polynomials in several variables, introduced by Koornwinder (1992), that generalize the Askey-Wilson polynomials. They are the Macdonald polynomials attached to the non-reduced affine root system of type (C∨
n, C_n), and in particular satisfy (Diejen 1996, Sahi 1999) analogues of Macdonald's conjectures (Macdonald 2003, Chapter 5.3). In addition Jan Felipe van Diejen showed that the Macdonald polynomials associated to any classical root system can be expressed as limits or special cases of Koornwinder polynomials and found complete sets of concrete commuting difference operators diagonalized by them (Diejen 1995). Furthermore there is a large class of interesting families of multivariable orthogonal polynomials associated with classical root systems which are degenerate cases of the Koornwinder-Macdonald polynomials (Diejen 1999). The Koornwinder-Macdonald polynomials have also been studied with the aid of affine Hecke algebras (Noumi 1995, Sahi 1999, Macdonald 2003).

The Koornwinder polynomial in n variables associated to the partition λ is the unique Laurent polynomial invariant under permutation and inversion of variables, with leading monomial x^λ, and orthogonal with respect to the density

$\prod_{1\le i<j\le n} \frac{(x_i x_j,x_i/x_j,x_j/x_i,1/x_ix_j;q)_\infty}{(t x_ix_j,t x_i/x_j,t x_j/x_i,t/x_ix_j;q)_\infty} \prod_{1\le i\le n} \frac{(x_i^2,1/x_i^2;q)_\infty}{(a x_i,a/x_i,b x_i,b/x_i,c x_i,c/x_i,d x_i,d/x_i;q)_\infty}$

on the unit torus

$|x_1|=|x_2|=\cdots|x_n|=1$ ,

where the parameters satisfy the constraints

$|a|,|b|,|c|,|d|,|q|,|t|<1,$

and (x;q)_∞ denotes the infinite q-Pochhammer symbol. Here leading monomial x^λ means that μ≤λ for all terms x^μ with nonzero coefficient, where μ≤λ if and only if μ₁≤λ₁, μ₁+μ₂≤λ₁+λ₂, …, μ₁+…+μ_n≤λ₁+…+λ_n. Under further constraints that q and t are real and that a, b, c, d are real or, if complex, occur in conjugate pairs, the given density is positive.

For some lecture notes on Koornwinder polynomials from a Hecke algebra perspective see for example (Stokman 2004).

References

van Diejen, Jan F. (1995), Commuting difference operators with polynomial eigenfunctions, Compositio Math., 95, pp. 183–233, MR 1313873

van Diejen, Jan F. (1996), Self-dual Koornwinder-Macdonald polynomials, Invent. Math., 126, pp. 319–339, MR 1411136

van Diejen, Jan F. (1999), Properties of some families of hypergeometric orthogonal polynomials in several variables, Trans. Amer. Math. Soc., 351, pp. 233–70, MR 1433128

Koornwinder, Tom H. (1992), Askey-Wilson polynomials for root systems of type BC, Contemp. Math., 138, pp. 189–204, MR 1199128

Macdonald, I. G. (2003), Affine Hecke algebras and orthogonal polynomials, Cambridge Tracts in Mathematics, 157, Cambridge: Cambridge University Press, pp. x+175, doi:10.2277/0521824729, ISBN 9780521824729, MR 1976581

Noumi, M. (1995), "Macdonald-Koornwinder polynomials and affine Hecke rings" (in Japanese), Various Aspects of Hypergeometric Functions, Surikaisekikenkyusho Kokyuroku, 919, pp. 44–55, MR 1388325

Sahi, S. (1999), Nonsymmetric Koornwinder polynomials and duality, Ann. of Math.(2), 150, pp. 267–282, MR 1715325

Stokman, Jasper V. (2004), "Lecture notes on Koornwinder polynomials", Laredo Lectures on Orthogonal Polynomials and Special Functions, Adv. Theory Spec. Funct. Orthogonal Polynomials, Hauppauge, NY: Nova Sci. Publ., pp. 145–207, MR 2085855